|

Soundfile 5.9
Unmodified speech

Soundfile 5.10
Speech made half as long with a phase vocoder

Soundfile 5.11
Speech made twice as long with a phase vocoder

Soundfile 5.12
Speech transposed up an octave

Soundfile 5.13
Speech transposed down an octave
|
Perhaps the most
commonly used implementation of Fourier analysis in computer music is
a technique called the phase vocoder. What is called the phase
vocoder actually comprises a number of techniques for taking a time-domain
signal, representing it as a series of amplitudes, phases, and frequencies,
and manipulating this information and returning it to the time domain.
(Remember, Fourier analysis is the process of turning the list of samples
of our music function into a list of Fourier coefficients, which are complex
numbers that have phase and amplitude, and each corresponds to a frequency.)
Two of the most important ways that musicians have used the phase vocoder
technique are to use a sound’s Fourier representation to manipulate
its length without changing its pitch and, conversely, to change its pitch
without affecting its length. This is called time stretching and
pitch shifting.
Why should this even be difficult? Well, consider trying it in the time domain: play back, say, a 33 1/3 RPM record at 45 RPMs. What happens? You play the record faster, the needle moves through the grooves at a higher rate, and the sound is higher pitched (often called the "chipmunk" effect, possibly after the famous 1960s novelty records featuring Alvin and his friends). The sound is also much shorter: in this case, pitch is directly related to frequency—they’re both controlled by the same mechanism. A creative and virtuosic use of this technique is scratching as practiced by hip-hop, rap, and dance DJs.
|
|
|
Using the Phase Vocoder
Using the phase vocoder, we can realize Steve Reich’s piece (see Xtra bit 5.1), and a great many others. The phase vocoder allows us independent control over the time and the pitch of a sound.
How does this work? Actually, in two different ways: by changing the speed and changing the pitch.
To change the speed, or length, of a sound without changing its pitch,
we need to know something about what is called windowing. Remember
that when doing an FFT on a sound, we use what are called frames—time-delimited
segments of sound. Over each frame we impose a window: an amplitude envelope
that allows us to cross-fade one frame into another, avoiding problems
that occur at the boundaries of the two frames.
What are these problems? Well, remember that when we take an FFT of some
portion of the sound, that FFT, by definition, assumes that we’re
analyzing a periodic, infinitely repeating signal. Otherwise, it wouldn’t
be Fourier analyzable. But if we just chop up the sound into FFT-frames,
the points at which we do the chopping will be hard-edged, and we’ll
in effect be assuming that our periodic signal has nasty edges on both
ends (which will typically show up as strong high frequencies). So to
get around this, we attenuate the beginning and ending of our frame with
a window, smoothing out the assumed periodical signal. Typically, these
windows overlap at a certain rate (1/8, 1/4, 1/2 overlap), creating even
smoother transitions between one FFT frame and another.
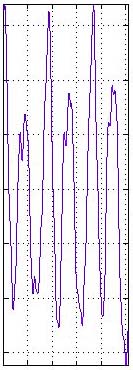 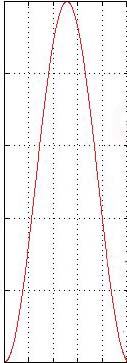 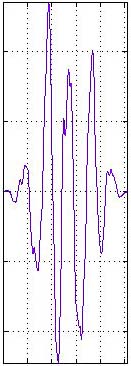
Figure 5.12 Why do we window
FFT frames? The image on the left shows the waveform that our FFT would
analyze without windowing—notice the sharp edges where the frame
begins and ends. The image in the middle is our window. The image on the
right shows the windowed waveform. By imposing a smoothing window on the
time domain signal and doing an FFT of the windowed signal, we de-emphasize
the high-frequency artifacts created by these sharp vertical drops at
the beginning and end of the frame.
Thanks to Jarno Seppänen <Jarno.Seppanen@nokia.com> Nokia Research
Center, Tampere, Finland, for these images.
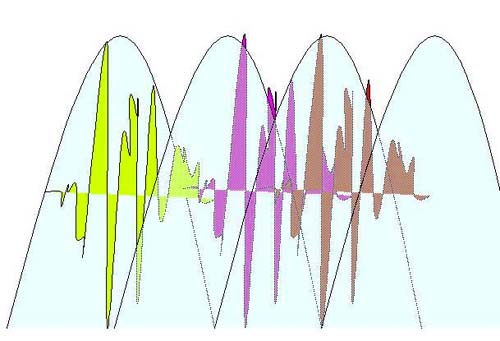
Figure 5.13 After we window a signal for the FFT, we overlap those windowed signals so that the original signal is reconstructed without the sharp edges.
By changing the length of the overlap when we resynthesize the signal, we can change the speed of the sound without affecting its frequency content (that is, the FFT information will remain the same, it’ll just be resynthesized at a "larger" frame size). That’s how the phase vocoder typically changes the length of a sound.
What about changing the pitch? Well, it’s easy to see that with
an FFT we get a set of amplitudes that correspond to a given set of frequencies.
But it’s clear that if, for example, we have very strong amplitudes
at 100 Hz, 200 Hz, 300 Hz, 400 Hz, and so on, we will perceive a strong
pitch at 100 Hz. What if we just take the amplitudes at all frequencies
and move them "up" (or down) to frequencies twice as high (or
as low)? What we’ve done then is re-create the frequency/amplitude
relationships starting at a higher frequency—changing the perceived
pitch without changing the frequency.
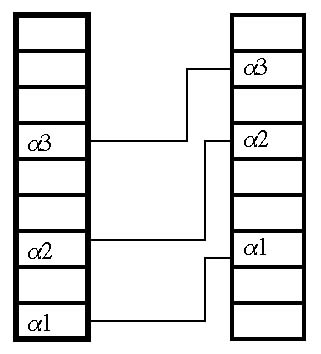
Figure 5.14 Two columns of FFT bins. These bins divide the Nyquist frequency evenly. In other words, if we were sampling at 10 kHz and we had 100 FFT bins (both these numbers are rather silly, but they’re arithmetically simple), our Nyquist frequency would be 5 kHz, and the bin width would be 50 Hz.
Each of these frequency bins has its own amplitude, which is the
strength or energy of the spectra at that frequency (or more precisely,
the average energy in that frequency range). To implement a pitch shift
in a phase vocoder, the amplitudes in the left column are shifted up to
higher frequencies in the right column. This operation shifts 1 spectra
in the left bin to a higher frequency in the right bin.
The phase vocoder technique actually works just fine, though for radical
pitch/time deformations we get some problems (usually called "phasiness").
These techniques work better for slowly changing harmonic sounds and for
simpler pitch/time relationships (integer multiples). Still, the phase
vocoder works well enough, in general, for it to be a widely used technique
in both the commercial and the artistic sound worlds.
|

